Backtracking

정의

백트래킹은 문제를 Brute force 방법의 일종으로, 문제를 재귀적으로 풀어내서 점진적으로 해결책을 마련하는 방법이다.

 

Example

Knight's tour 문제를 보자.

 

 

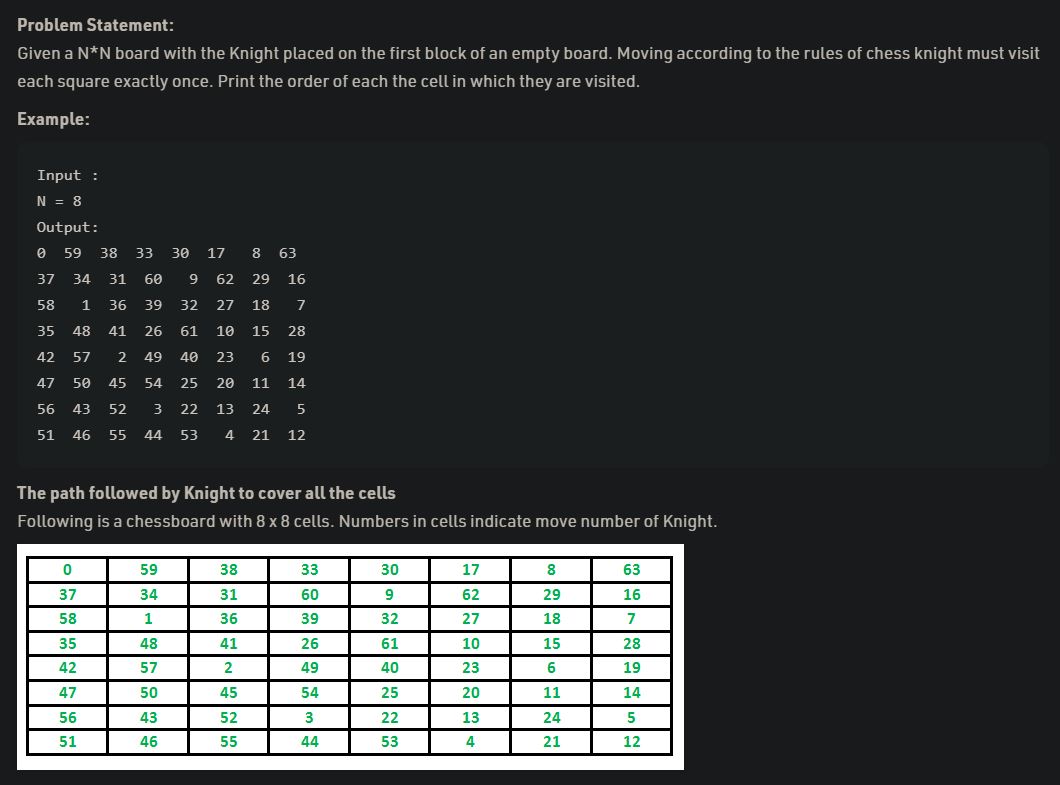
N*N의 보드에서 체스말인 나이트가 이 보드를 전부 방문한다고 할 때, 나이트가 방문한 순서를 print하는 문제이다.

 

푸는 방법에는 두가지가 있는데

 

하나는 모든 경우의 수를 생성하고 조건을 만족하는지를 check하는 Naive Algorithm

두번째는 Backtracking이다.

 

1. Naive Approach

모든 경우를 생성하고, 조건에 만족하는지를 체크하는 방법이다.

while there are untried tour {
  generate the next tour
  if this tour covers all squares {
    print this path;
  }
}

 

 

2. Backtracking

다음과 같은 절차를 따른다.

1. 아이템을 추가한다.

2. 만약 아이템이 조건에 부합하지 않으면 아이템을 제거하고 다른 방법을 시도한다.

3. 만약 다른 모든 방법을 시도했는데도 적합한 답이 없다면 false를 리턴한다.

 

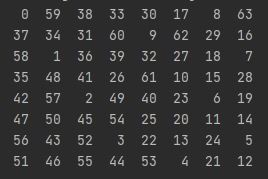
If all square are visited
  print the solution
else
  a) Add one of the next moves to solution vector and recursively check
  if this move leads to a solution. (A knight can make maximum eight moves.
  We choose one of the 8 moves in this step).
  b) It the move chosen in the above step doesnt lead to a solution then
  remove this move from the solution vector and try other alternative moves.
  c) If none of the alternatives work then return false (Returning false
  will remove the previously added item in recursion and if false is returned
  by the initial call of recursion then "no sulution exist"

 

 

public class KnightTour {
    static int N = 8;
 
    // A utility function to check if i, j are valid indexed for N*N chessboard
    static boolean isSafe(int x, int y, int sol[][]) {
        return (
                    x >= 0 && x < N &&
                    y >= 0 && y < N &&
                    sol[x][y] == -1
                );
    }
 
    // A utility function to print solution matrix sol[N][N]
    static void printSolution(int sol[][]) {
        for(int x = 0; x < N; x++) {
            for(int y = 0; y < N; y++) {
                System.out.printf("%3d ", sol[x][y] );
            }
            System.out.println();
        }
    }
 
    /*
         This function solves the knight tour problem using Backtracking.
         This function mainly uses solveKUtil() to solve the problem.
         It return false if no complete tour is possible,
         otherwise return true and prints the tour.
         Pleases note that there may be more than one solution,
         this function prints one of the feasible solutions.
     */
    static boolean solveKT() {
        int sol[][] = new int[8][8];
 
        // Initialize of solution matrix
        for(int x = 0; x < N; x++) {
            for(int y = 0; y < N; y++) {
                sol[x][y] = -1;
            }
        }
 
        /*
            xMove[] and yMove[] define next move of Knight.
            xMove[] is for next value of x coordinate.
            yMove[] is for next value of y coordinate.
         */
        int xMove[] = {2, 1, -1, -2, -2, -1, 1, 2};
        int yMove[] = {1, 2, 2, 1, -1, -2, -2, -1};
 
        // Since the Knight is initially at the first block
        sol[0][0] = 0;
 
        // Start from 0,0 and explore all tours using solveKTUtil()
        if(!solveKTUtil(0, 0, 1, sol, xMove, yMove)) {
            System.out.println("Solution does not exist");
            return false;
        }
        else {
            printSolution(sol);
            return true;
        }
    }
 
    // A recursive utility function to solve Knight Tour problem
    static boolean solveKTUtil(int x, int y, int movei, int sol[][], int xMove[], int yMove[]) {
        int k, next_x, next_y;
        if(movei == N*N)
            return true;
 
        // Try all next moves from the current coordinate x, y
        for(k = 0; k < 8; k++) {
            next_x = x + xMove[k];
            next_y = y + yMove[k];
 
            if(isSafe(next_x, next_y, sol)) {
                sol[next_x][next_y] = movei;
                if(solveKTUtil(next_x, next_y, movei+1, sol, xMove, yMove)) {
                    return true;
                }
                else {
                    sol[next_x][next_y] = -1; // backtracking
                }
            }
        }
        return false;
    }
 
    public static void main(String args[])
    {
        // Function Call
        solveKT();
    }
 
// This code is contributed by Abhishek Shankhadhar
}
 

 

Output:

 

---

Reference

www.geeksforgeeks.org/the-knights-tour-problem-backtracking-1/

The Knight's tour problem | Backtracking-1 - GeeksforGeeks